㚉读音,㚉部首,㚉吉凶分析及解释

汉字 㚉

读音 读gǔ的字

拼音 gu

部外笔 部外笔画是5画的字

部 部首是夕的字

总笔画 共8画的字

结构 上下结构的字

笔顺读 横折、撇、撇、横折、点、撇、横折、点

五笔 EQQU

仓颉 NSNIN

郑 YMRR

四角 17207

英汉翻译 (corrupted form) to make a profit on sell and buy,the profit in business,(interchangeable嬴) a overplus,gain,profit,abundance

异体字 夃

注音 ㄍㄨˇ

统一码 3689

方言

◎ 粤语：gu2

康熙字典

㚉【丑集下】【夕部】 康熙筆画：8画，部外筆画：5画

字之譌。

说文解字

说文解字

夃【卷五】【夂部】

秦以市買多得爲夃。从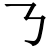从夂，益至也。从乃。《詩》曰：“我夃酌彼金罍。”古乎切〖注〗臣鉉等曰：乃，難意也。

说文解字注

（夃）秦人巿買多得爲夃。爲當作謂之二字。此秦人語也。方言不載。从乃。从夂。益至也。說从乃夂之意。乃夂者、徐徐而益至也。古乎切。五部。詩曰。我夃酌彼金罍。周南文。今毛詩作姑酌。傳曰。姑、且也。許所據者毛詩古本。今作姑者、後人以今字易之也。如尙書壁中古文本作無有作、本作黎民俎飢之類。夃者、姑之假借字。如俎者、好阻之假借字。玉篇曰。夃、今作沽。引論語求善價而夃諸。未審其所本之論語。

Tags： 㚉读gǔ的字部外笔画是5画的字部首是夕的字共8画的字上下结构的字

文章版权声明：除非注明，否则均为小美知识分享小站原创文章，转载或复制请以超链接形式并注明出处。